Levenberg-Marquardt optimization class. More...

#include <LevenbergMarquardtOptimizer.h>

Public Member Functions
	LevenbergMarquardtOptimizer (Model *model, int num_obs, int num_params, double lambda0, double tol_grad, double tol_inc, int max_iter)
	Construct a new LevenbergMarquardtOptimizer object.

Eigen::Matrix< double, Eigen::Dynamic, 1 >	run (Eigen::Matrix< double, Eigen::Dynamic, 1 > alpha, std::vector< std::vector< double > > &y_obs, std::vector< std::vector< double > > &dy_obs)
	Run the optimization algorithm.

Detailed Description

Levenberg-Marquardt optimization class.

The 0D residual (assuming no time-dependency in parameters) is

$\boldsymbol{r}(\boldsymbol{\alpha}, \boldsymbol{y}, \boldsymbol{\dot{y}}) = \boldsymbol{E}(\boldsymbol{\alpha}, \boldsymbol{y}) \cdot \dot{\boldsymbol{y}}+\boldsymbol{F}(\boldsymbol{\alpha}, \boldsymbol{y}) \cdot \boldsymbol{y}+\boldsymbol{c}(\boldsymbol{\alpha}, \boldsymbol{y})$

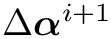
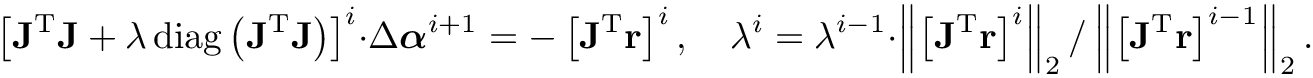
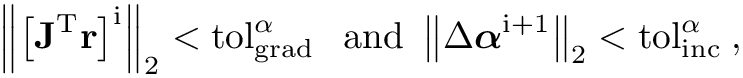
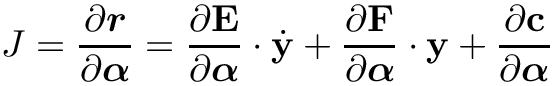
with solution vector $\boldsymbol{y} \in \mathbb{R}^{N}$ (flow and pressure at nodes), LPN parameters $\boldsymbol{\alpha} \in \mathbb{R}^{P}$ , system matrices $\boldsymbol{E},\boldsymbol{F} \in \mathbb{R}^{NxN}$ , and system vector $\boldsymbol{c} \in \mathbb{R}^{N}$ .

The least squares problem can be formulated as

$\min _\alpha S, \quad \mathrm { with } \quad S=\sum_i^D r_i^2\left(\boldsymbol{\alpha}, y_i, \dot{y}_i\right)$

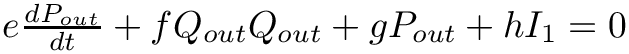
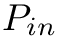
with given solution vectors $\boldsymbol{y}$ , $\boldsymbol{\dot{y}}$ at all datapoints . The parameter vector is iteratively improved according to

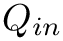
$\boldsymbol{\alpha}^{i+1}=\boldsymbol{\alpha}^{i}+\Delta \boldsymbol{\alpha}^{i+1}$

wherein the increment 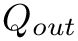$\Delta \boldsymbol{\alpha}^{i+1}$ is determined by solving the following system:

$\left[\mathbf{J}^{\mathrm{T}} \mathbf{J}+\lambda \operatorname{diag}\left(\mathbf{J}^{\mathrm{T}} \mathbf{J}\right)\right]^{i} \cdot \Delta \boldsymbol{\alpha}^{i+1}=-\left[\mathbf{J}^{\mathrm{T}} \mathbf{r}\right]^{i}, \quad \lambda^{i}=\lambda^{i-1} \cdot\left\|\left[\mathbf{J}^{\mathrm{T}} \mathbf{r}\right]^{i}\right\|_2 /\left\|\left[\mathbf{J}^{\mathrm{T}} \mathbf{r}\right]^{i-1}\right\|_2.$

The algorithm terminates when the following tolerance thresholds are reached

$\left\|\left[\mathbf{J}^{\mathrm{T}} \mathbf{r}\right]^{\mathrm{i}}\right\|_2<\operatorname{tol}_{\text {grad }}^\alpha \text { and }\left\|\Delta \boldsymbol{\alpha}^{\mathrm{i}+1}\right\|_2<\mathrm{tol}_{\text {inc }}^\alpha,$

The Jacobian is derived from the residual as

$J = \frac{\partial \boldsymbol{r}}{\partial \boldsymbol{\alpha}} = \frac{\partial \mathbf{E}}{\partial \boldsymbol{\alpha}} \cdot \dot{\mathbf{y}}+\frac{\partial \mathbf{F}}{\partial \boldsymbol{\alpha}} \cdot \mathbf{y}+\frac{\partial \mathbf{c}}{\partial \boldsymbol{\alpha}}$

Constructor & Destructor Documentation

◆ LevenbergMarquardtOptimizer()

LevenbergMarquardtOptimizer::LevenbergMarquardtOptimizer	(	Model *	model,
		int	num_obs,
		int	num_params,
		double	lambda0,
		double	tol_grad,
		double	tol_inc,
		int	max_iter )

Construct a new LevenbergMarquardtOptimizer object.

Parameters

model	The 0D model
num_obs	Number of observations in optimization
num_params	Number of parameters in optimization
lambda0	Initial damping factor
tol_grad	Gradient tolerance
tol_inc	Parameter increment tolerance
max_iter	Maximum iterations

Member Function Documentation

◆ run()

Eigen::Matrix< double, Eigen::Dynamic, 1 > LevenbergMarquardtOptimizer::run	(	Eigen::Matrix< double, Eigen::Dynamic, 1 >	alpha,
		std::vector< std::vector< double > > &	y_obs,
		std::vector< std::vector< double > > &	dy_obs )

Run the optimization algorithm.